Understanding Chord Secant Tangent: A Comprehensive Guide

Have you ever pondered the intriguing concepts of "chord secant tangent" and their significance in mathematics and geometry? These terms are not just technical jargon but are foundational elements that play a crucial role in the study of circles and their properties. Understanding these concepts is essential for grasping the fundamentals of geometry and for solving complex mathematical problems that involve circles. Whether you're a student, a teacher, or just someone with a keen interest in mathematics, exploring the intricacies of chords, secants, and tangents can provide valuable insights into the world of geometry.

The world of mathematics is vast and filled with fascinating concepts that shape our understanding of the universe. Among these concepts, the "chord secant tangent" provides a unique perspective on the properties of circles and how they interact with lines. These elements are not only essential for academic purposes but also have practical applications in fields such as engineering, architecture, and physics. By delving into the details of chords, secants, and tangents, we can appreciate the elegance and precision of mathematical principles that govern the shapes and structures around us.

In this comprehensive guide, we will explore the definitions, properties, and applications of chords, secants, and tangents. We will also examine how these concepts are interconnected and how they contribute to our understanding of geometry. With clear explanations, illustrative examples, and insightful discussions, this article aims to provide a thorough understanding of the "chord secant tangent" and its significance in mathematics. So, let's embark on this enlightening journey into the heart of geometry and discover the wonders of chords, secants, and tangents.

Table of Contents

• Definition of Chord, Secant, and Tangent
• Properties and Characteristics
• Geometric Relations and Interactions
• Practical Applications in Real Life
• Mathematical Formulas and Theorems
• Chord Theorems and Their Proofs
• Secant Theorems and Their Proofs
• Tangent Theorems and Their Proofs
• Historical Perspective and Evolution
• Effective Teaching Methods
• Challenges and Misconceptions
• Role of Technology in Learning
• Problem-Solving Techniques
• Future Implications and Developments
• Frequently Asked Questions
• Conclusion

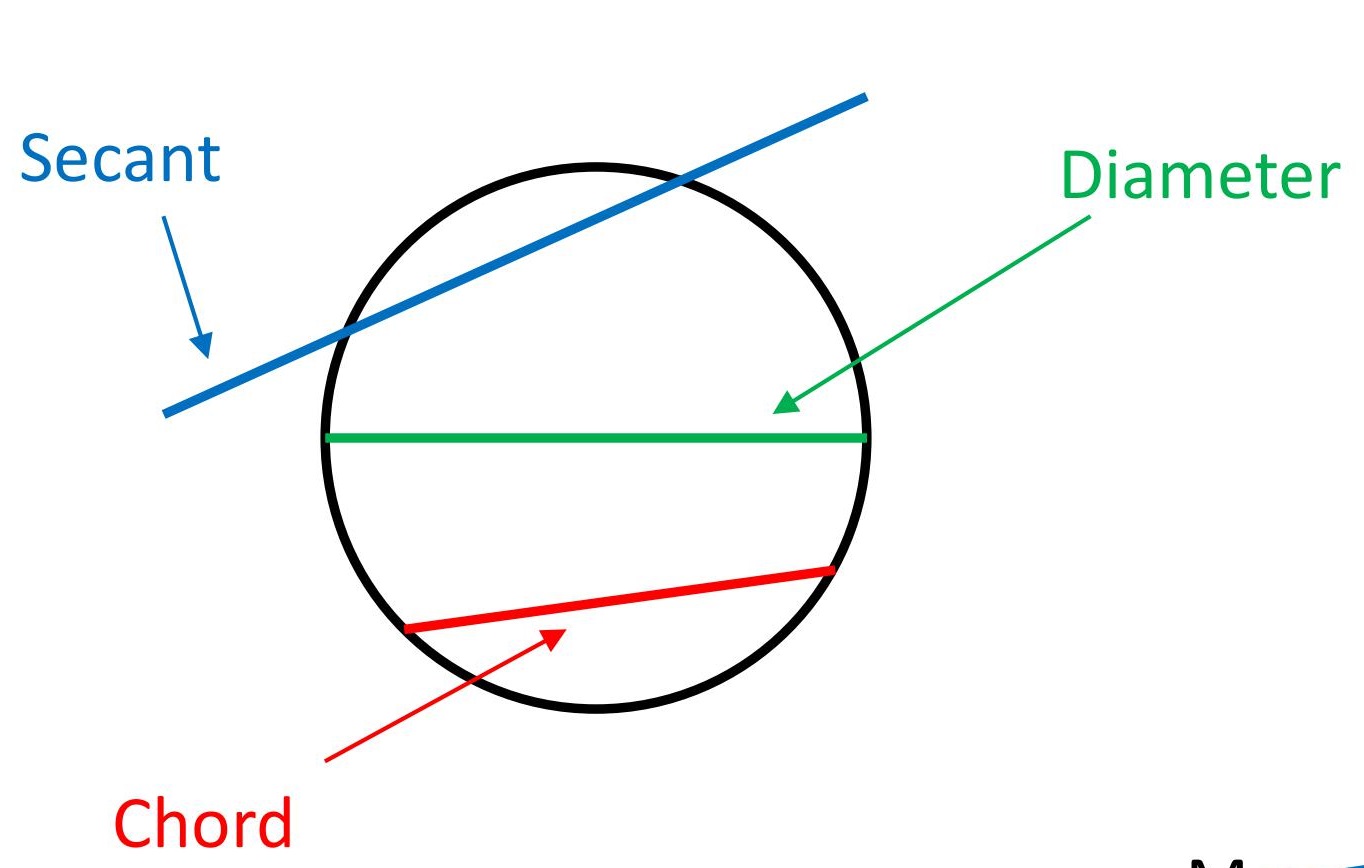
Definition of Chord, Secant, and Tangent

In the realm of geometry, a chord is a straight line segment whose endpoints both lie on the circle. It is one of the fundamental elements in the study of circular geometry. A chord divides the circle into two arcs, providing a basis for further geometric analysis. The longest chord of a circle is the diameter, which passes through the center of the circle and divides it into two equal halves.

A secant, on the other hand, is a line that intersects a circle at two distinct points. Secants extend beyond the circle, unlike chords, which are confined within the circle's boundary. Secants play a crucial role in various geometric theorems, providing insights into the relationships between different parts of a circle.

Lastly, a tangent is a line that touches the circle at exactly one point, known as the point of tangency. Unlike secants and chords, tangents do not intersect the circle at multiple points. They form a right angle with the radius drawn to the point of tangency. Tangents are essential in understanding the properties of circles and are often used in calculations involving angles and distances.

Properties and Characteristics

Chords, secants, and tangents each possess unique properties that define their behavior and relationships within a circle. Understanding these properties is vital for solving geometric problems and for appreciating the intricate beauty of mathematics.

Properties of Chords: Chords have several interesting properties. For example, equal chords are equidistant from the center of the circle, and a perpendicular drawn from the center of the circle to a chord bisects the chord. Additionally, the angle subtended by a chord at the center of the circle is twice the angle subtended by the same chord on the circle's remaining part.

Characteristics of Secants: Secants exhibit unique characteristics that distinguish them from chords and tangents. One of the key properties of secants is that they can form angles with the circle's radius, leading to the development of important theorems such as the secant-secant theorem. Secants also play a role in establishing relationships between different segments within a circle.

Unique Features of Tangents: Tangents have distinct features that set them apart from other lines associated with circles. The most notable property of tangents is that they are perpendicular to the radius at the point of tangency. This perpendicularity is fundamental to numerous geometric proofs and calculations. Furthermore, tangents drawn from an external point to a circle are equal in length, which is a crucial aspect of tangent properties.

Geometric Relations and Interactions

The interplay between chords, secants, and tangents gives rise to fascinating geometric relations that are foundational to the study of circles. These interactions provide insights into the symmetrical and proportional nature of circles, enabling mathematicians to solve complex problems with ease.

Interactions Between Chords and Secants: Chords and secants are interconnected through various geometric principles. A noteworthy relationship is the chord-secant theorem, which states that if a secant and a tangent are drawn from an external point to a circle, then the square of the length of the tangent segment is equal to the product of the lengths of the segments formed by the secant. This theorem highlights the proportionality and balance inherent in circle geometry.

Interactions Between Secants and Tangents: Secants and tangents also have significant relationships that contribute to the understanding of circle properties. For instance, the angle formed between a tangent and a secant drawn from the same external point is equal to the angle formed between the secant and the chord inside the circle. This relationship is a testament to the harmonious interplay between different elements within a circle.

Chords and Tangents in Harmony: The relationship between chords and tangents is characterized by symmetry and balance. The perpendicularity of tangents to the radius at the point of tangency plays a crucial role in establishing these geometric relationships. The angle subtended by a chord at the point of tangency is equal to the angle subtended by the chord at the circle's center, demonstrating the interconnectedness of these elements.

Practical Applications in Real Life

The concepts of chords, secants, and tangents extend beyond theoretical mathematics and have practical applications in various fields. These applications demonstrate the versatility and relevance of these geometric elements in solving real-world problems.

Applications in Engineering: In engineering, the principles of chords, secants, and tangents are used in the design and analysis of structures. For example, understanding the properties of tangents is essential in the construction of roads and bridges, where precise measurements and angles are crucial for ensuring stability and safety.

Role in Architecture: Architects often utilize the concepts of chords and tangents to create aesthetically pleasing and structurally sound designs. The symmetry and balance inherent in these geometric elements are reflected in the construction of buildings and monuments, where angles and proportions are carefully calculated to achieve the desired visual effect.

Importance in Physics: In physics, the principles of chords, secants, and tangents are applied in the study of motion and forces. For instance, the trajectory of a projectile can be analyzed using the concepts of tangents and secants, providing insights into the object's path and behavior.

Mathematical Formulas and Theorems

Chords, secants, and tangents are governed by various mathematical formulas and theorems that provide a framework for understanding their properties and relationships. These formulas are essential tools for solving geometric problems and for deriving new insights into circle geometry.

Key Formulas for Chords: One of the fundamental formulas associated with chords is the chord length formula, which relates the length of a chord to the radius and the angle subtended by the chord at the center. This formula is crucial for calculating distances and angles within a circle.

Secant and Tangent Theorems: The secant-tangent theorem is a pivotal theorem in circle geometry, establishing a relationship between the lengths of tangent and secant segments drawn from an external point. This theorem is a cornerstone of geometric proofs and is widely used in problem-solving.

Applications of Tangent Properties: The properties of tangents, such as their perpendicularity to the radius, are encapsulated in various theorems that provide a deeper understanding of circle geometry. These theorems are instrumental in proving theorems and in deriving new geometric insights.

Chord Theorems and Their Proofs

Chord theorems are an integral part of circle geometry, providing valuable insights into the properties and relationships of chords. These theorems are supported by rigorous mathematical proofs that highlight the logical and systematic nature of geometry.

Theorem of Equal Chords: One of the fundamental chord theorems states that equal chords of a circle are equidistant from the center. This theorem is proven by considering the perpendicular distance from the center to the chord and demonstrating the equality of these distances for equal chords.

Angle Subtended by a Chord: Another key theorem involves the angle subtended by a chord at the center of the circle. This theorem asserts that the angle subtended by a chord at the center is twice the angle subtended by the same chord at any point on the circumference. This theorem is proven using principles of symmetry and proportionality.

Perpendicular Bisector Theorem: The perpendicular bisector theorem states that the perpendicular drawn from the center of a circle to a chord bisects the chord. This theorem is proven by considering the symmetry of the circle and the properties of right angles.

Secant Theorems and Their Proofs

Secant theorems are essential for understanding the relationships between secants and other elements within a circle. These theorems are supported by mathematical proofs that demonstrate the logical coherence of geometric principles.

Secant-Secant Theorem: The secant-secant theorem establishes a relationship between the lengths of segments formed by two secants drawn from an external point. This theorem is proven by considering the proportionality of the segments and using the properties of similar triangles.

Angle Formed by Secants: Another important secant theorem involves the angle formed between two secants drawn from an external point. This theorem states that the angle formed is equal to half the difference of the intercepted arcs, and it is proven using principles of symmetry and congruence.

Secant-Tangent Theorem: The secant-tangent theorem is a pivotal theorem that establishes a relationship between the lengths of tangent and secant segments drawn from an external point. This theorem is proven using the properties of right angles and the principles of proportionality.

Tangent Theorems and Their Proofs

Tangent theorems are fundamental to the study of circle geometry, providing insights into the properties and relationships of tangents. These theorems are supported by rigorous mathematical proofs that highlight the precision and elegance of geometric principles.

Tangent-Radius Theorem: One of the fundamental tangent theorems states that a tangent to a circle is perpendicular to the radius drawn to the point of tangency. This theorem is proven by considering the properties of right angles and the definition of a tangent.

Equal Tangents Theorem: Another key tangent theorem involves the equality of tangents drawn from an external point to a circle. This theorem asserts that the tangents are equal in length, and it is proven by considering the properties of congruent triangles and the symmetry of the circle.

Angle Formed by Tangents: The angle formed between two tangents drawn from an external point is equal to half the difference of the intercepted arcs. This theorem is proven using principles of symmetry and congruence and is instrumental in solving geometric problems involving tangents.

Historical Perspective and Evolution

The concepts of chords, secants, and tangents have a rich historical background, with their origins dating back to ancient civilizations. Understanding the historical evolution of these concepts provides valuable insights into the development of mathematical thought and the progression of geometric principles.

Ancient Origins: The study of circles and their properties can be traced back to ancient Greek mathematicians such as Euclid and Archimedes. These pioneers laid the groundwork for the development of geometric principles, including the concepts of chords, secants, and tangents. Their contributions to mathematics have had a lasting impact on the field and continue to influence modern mathematical thought.

Medieval Advancements: During the medieval period, mathematicians in the Islamic world made significant advancements in the study of geometry. They expanded upon the work of ancient Greek mathematicians and developed new theorems and formulas related to chords, secants, and tangents. These contributions played a crucial role in the advancement of mathematical knowledge and paved the way for further developments in the field.

Modern Developments: In the modern era, the study of chords, secants, and tangents has evolved to incorporate new mathematical techniques and technologies. The development of analytic geometry and calculus has provided new tools for understanding the properties and relationships of these geometric elements. Today, the study of chords, secants, and tangents continues to be an essential part of mathematical education and research.

Effective Teaching Methods

Teaching the concepts of chords, secants, and tangents can be challenging, but with effective teaching methods, educators can engage students and foster a deep understanding of these geometric principles.

Interactive Learning: Incorporating interactive learning techniques, such as hands-on activities and visual aids, can help students grasp the concepts of chords, secants, and tangents. Using models and diagrams to illustrate these concepts can make abstract ideas more tangible and enhance students' comprehension.

Real-World Applications: Demonstrating the real-world applications of chords, secants, and tangents can make learning more relevant and engaging for students. By connecting these concepts to everyday experiences and practical problems, educators can help students see the value and importance of understanding geometry.

Technology Integration: Utilizing technology in the classroom, such as geometry software and online resources, can provide additional support for teaching chords, secants, and tangents. These tools can offer dynamic visualizations and interactive exercises that reinforce students' understanding and promote active learning.

Challenges and Misconceptions

Students often encounter challenges and misconceptions when learning about chords, secants, and tangents. Addressing these issues is essential for fostering a thorough understanding of geometric principles.

Common Misconceptions: One common misconception is the confusion between secants and tangents, as both involve lines intersecting a circle. Clarifying the differences between these concepts and emphasizing their unique properties can help students overcome this confusion.

Understanding Proportionality: Grasping the concept of proportionality in the relationships between chords, secants, and tangents can be challenging for students. Providing clear explanations and examples of how these elements interact proportionally within a circle can aid in comprehension.

Visualizing Geometric Relationships: Visualizing the relationships between chords, secants, and tangents can be difficult for some students. Using diagrams and models to illustrate these relationships can enhance students' spatial reasoning and help them better understand geometric principles.

Role of Technology in Learning

Technology plays a significant role in enhancing the learning experience for students studying chords, secants, and tangents. By leveraging digital tools and resources, educators can create a more engaging and interactive learning environment.

Geometry Software: Geometry software allows students to explore and manipulate geometric shapes, providing a hands-on learning experience. These tools enable students to visualize the properties and relationships of chords, secants, and tangents, making abstract concepts more accessible.

Online Resources: The internet offers a wealth of resources for teaching and learning geometry, including tutorials, videos, and interactive exercises. These resources can supplement traditional classroom instruction and provide students with additional opportunities to practice and reinforce their understanding of chords, secants, and tangents.

Virtual Reality: Emerging technologies such as virtual reality offer exciting possibilities for teaching geometry. By creating immersive environments where students can explore geometric concepts, educators can provide a unique and engaging learning experience that enhances students' spatial reasoning and understanding.

Problem-Solving Techniques

Problem-solving is an essential skill in mathematics, and developing effective techniques for solving problems involving chords, secants, and tangents is crucial for students' success.

Analytical Approach: Encouraging students to adopt an analytical approach to problem-solving can help them systematically break down complex problems involving chords, secants, and tangents. By analyzing the given information and identifying relevant formulas and theorems, students can develop a clear strategy for solving the problem.

Visualization Techniques: Visualization is a powerful tool for solving geometric problems. Encouraging students to draw diagrams and use models to represent problems involving chords, secants, and tangents can help them better understand the relationships and interactions within the circle.

Practice and Reinforcement: Consistent practice and reinforcement are essential for developing problem-solving skills. Providing students with a variety of problems involving chords, secants, and tangents can help them apply their knowledge and build confidence in their ability to solve complex geometric problems.

Future Implications and Developments

The study of chords, secants, and tangents continues to evolve, with new developments and implications for the future of mathematics and education.

Advancements in Geometry: As mathematical research continues to advance, new insights and discoveries related to chords, secants, and tangents are likely to emerge. These developments will contribute to a deeper understanding of geometric principles and expand the scope of mathematical knowledge.

Educational Innovations: Innovations in education, such as personalized learning and adaptive technology, have the potential to transform the way students learn about chords, secants, and tangents. By providing tailored learning experiences that cater to individual students' needs, these innovations can enhance student engagement and achievement.

Interdisciplinary Applications: The principles of chords, secants, and tangents have applications beyond mathematics and can be integrated into interdisciplinary studies. By exploring the connections between geometry and other fields such as art, engineering, and computer science, educators can provide students with a broader and more holistic understanding of these geometric concepts.

Frequently Asked Questions

1. What is the difference between a chord and a secant?
A chord is a line segment with both endpoints on a circle, whereas a secant is a line that intersects a circle at two points and extends beyond the circle.

2. How is a tangent different from a secant?
A tangent touches a circle at exactly one point, while a secant intersects a circle at two points.

3. What is the significance of the tangent-secant theorem?
The tangent-secant theorem establishes a relationship between the lengths of a tangent and a secant drawn from an external point to a circle, highlighting the proportionality and balance within circle geometry.

4. How do chords, secants, and tangents relate to real-world applications?
Chords, secants, and tangents have practical applications in fields such as engineering, architecture, and physics, where they are used to design structures, analyze motion, and solve real-world problems.

5. What are some effective teaching methods for chords, secants, and tangents?
Effective teaching methods include interactive learning, real-world applications, and technology integration, which engage students and enhance their understanding of geometric principles.

6. How can technology aid in learning about chords, secants, and tangents?
Technology, such as geometry software and online resources, provides dynamic visualizations and interactive exercises that support learning and reinforce students' understanding of these concepts.

Conclusion

In conclusion, the study of chords, secants, and tangents is a fundamental aspect of geometry, providing valuable insights into the properties and relationships of circles. These concepts have practical applications in various fields and continue to be an essential part of mathematical education and research. By understanding the definitions, properties, and interactions of chords, secants, and tangents, we can appreciate the elegance and precision of mathematical principles that govern the shapes and structures around us. As we continue to explore and develop new insights into these geometric elements, we can look forward to the future implications and advancements that will shape our understanding of mathematics and its applications in the world.

For further reading on circle geometry and related topics, consider exploring resources from reputable educational institutions and online platforms.