The Comprehensive Guide To Understanding The Length Of A Vector R

Vectors are fundamental elements in mathematics and physics, representing quantities that have both magnitude and direction. Among various aspects of vectors, the length or magnitude is a critical concept. The "length of a vector r" is a term often encountered in physics, engineering, and computer science when analyzing forces, velocities, or any other vector quantities. Understanding the length of a vector is essential for solving problems that involve distance, speed, or force, making it a foundational concept in both theoretical and applied sciences.

Determining the length of a vector involves understanding its components and how they interact spatially. Vectors can exist in two-dimensional or three-dimensional spaces, and their length is derived using the Pythagorean Theorem. This theorem is a cornerstone of geometry, providing a method to calculate the hypotenuse of a right triangle. Translating this concept to vectors, the length is akin to the hypotenuse, calculated using the squares of the vector's components. This calculation is not just limited to geometric interpretation but extends to various applications, including computer graphics, where vectors dictate motion and orientation.

Exploring the length of a vector r provides insights into how vectors operate within different fields of study. Whether in physics, where they describe forces acting on an object, or in computer graphics, where they define the position and movement of objects, knowing how to compute and interpret vector length is crucial. This article delves into the comprehensive understanding of vector length, offering clear explanations, examples, and applications to ensure a robust grasp of this essential concept. By the end, readers will have a solid understanding of how to calculate and apply the length of a vector in various contexts.

Table of Contents

• Understanding Vectors
• Components of a Vector
• Calculation of Vector Length
• Length of a Vector in 2D
• Length of a Vector in 3D
• Applications in Physics
• Applications in Computer Graphics
• Applications in Engineering
• Vector Length in Calculus
• Common Mistakes and Misconceptions
• Advanced Concepts Related to Vector Length
• Frequently Asked Questions
• Conclusion

Understanding Vectors

Vectors are mathematical entities used to represent quantities that have both magnitude and direction. Unlike scalars, which only have magnitude, vectors indicate direction, making them crucial in fields like physics and engineering. A vector is typically represented as an arrow, where the length of the arrow corresponds to the vector's magnitude, and the arrow direction indicates the vector's direction.

Vectors can be represented in various forms, such as geometric, component, or matrix form. Geometrically, vectors are depicted as arrows in a coordinate system, with their tails at the origin and heads pointing towards the endpoint. In component form, vectors are expressed using coordinates, such as (x, y) for two-dimensional vectors and (x, y, z) for three-dimensional vectors. Understanding these representations is key to grasping the concept of vector length.

Vectors are foundational in describing physical phenomena, such as forces acting on an object, velocity, and acceleration. They are also essential in computer graphics, where they represent positions, directions, and transformations of objects in a virtual space. By understanding vectors and their properties, such as length, one can solve complex problems in various scientific and engineering fields.

Components of a Vector

The components of a vector are the projections of the vector along the axes of a coordinate system. For a two-dimensional vector, the components are the horizontal (x) and vertical (y) projections. In three dimensions, an additional z component represents the projection along the z-axis. These components help in breaking down a vector into simpler parts, making it easier to perform mathematical operations.

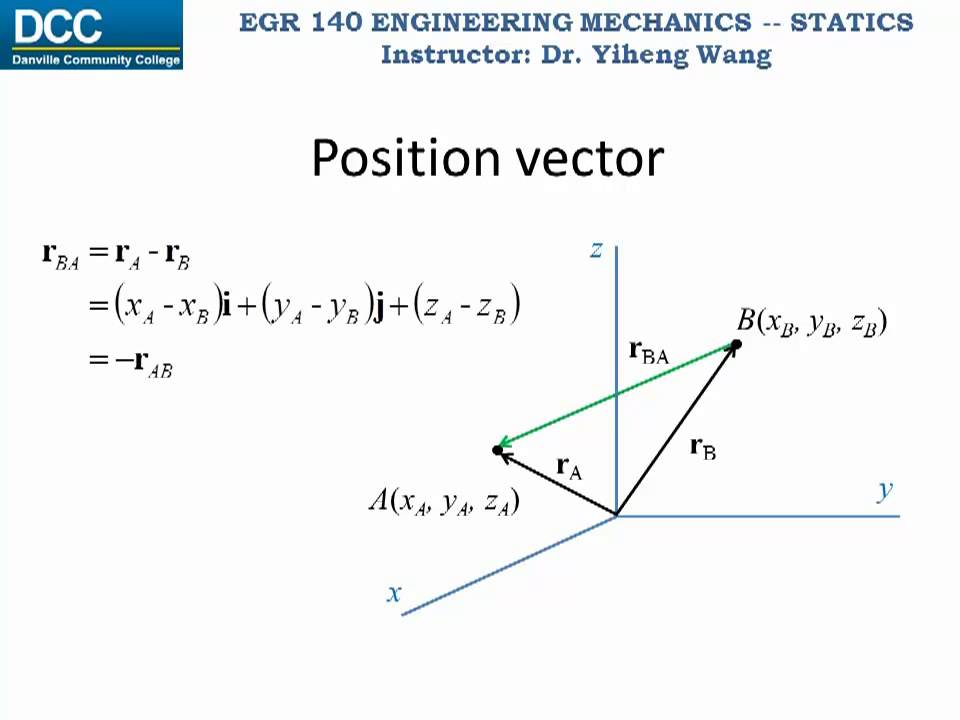
Mathematically, a vector's components can be represented as (x, y) in 2D or (x, y, z) in 3D. These components are crucial for calculating the vector's length and performing vector addition, subtraction, and scalar multiplication. The components are derived based on the vector's orientation in the coordinate system, and they determine the vector's magnitude and direction.

Understanding vector components is essential for calculating vector length, which involves determining the magnitude of the vector based on its components. This understanding also aids in visualizing vector operations, such as addition, where vectors are added component-wise. Mastery of vector components and their role in vector length calculation provides a strong foundation for tackling more advanced vector-related concepts.

Calculation of Vector Length

The length or magnitude of a vector is a measure of how long the vector is. It is calculated using the Pythagorean Theorem, which relates the square of the hypotenuse of a right triangle to the sum of the squares of its other two sides. In the context of vectors, the hypotenuse is the vector's length, and the sides are its components.

For a two-dimensional vector (x, y), the length is calculated as √(x² + y²). This formula is derived from the geometric interpretation of the vector as a diagonal of a rectangle formed by its components. In three dimensions, the length is calculated as √(x² + y² + z²), accounting for the additional z component. These formulas provide a straightforward method to determine the vector's magnitude, which is essential for various applications.

Understanding the calculation of vector length is fundamental for solving problems involving vectors in physics, engineering, and computer graphics. It allows for the determination of distances, speeds, and forces, among other quantities, making it a versatile and crucial concept. Mastery of vector length calculation provides the skills necessary to tackle more complex vector operations and applications.

Length of a Vector in 2D

In two-dimensional space, vectors are represented by two components, typically denoted as (x, y). The length of a 2D vector is the distance from the origin to the point represented by the vector, calculated using the formula √(x² + y²). This formula is derived from the Pythagorean Theorem, which relates the sides of a right triangle to its hypotenuse.

To calculate the length of a 2D vector, one must first identify its components, which represent the vector's projections along the x and y axes. These components are squared and summed, and the square root of this sum gives the vector's length. This length is a scalar quantity, representing the vector's magnitude without regard to its direction.

The length of a 2D vector is essential for various applications, such as determining the distance between two points, calculating the speed of a moving object, or analyzing forces acting in a plane. Understanding this concept allows for the solution of numerous practical problems in mathematics, physics, and engineering, where vectors play a critical role.

Length of a Vector in 3D

In three-dimensional space, vectors have three components, typically denoted as (x, y, z). The length of a 3D vector is the distance from the origin to the point represented by the vector, calculated using the formula √(x² + y² + z²). This formula extends the Pythagorean Theorem to three dimensions, accounting for the additional z component.

Calculating the length of a 3D vector involves determining its components, representing the vector's projections along the x, y, and z axes. These components are squared and summed, and the square root of this sum gives the vector's length. This length is a scalar quantity, representing the vector's magnitude without regard to its direction.

The length of a 3D vector is crucial for applications involving spatial analysis, such as determining the distance between points in space, analyzing forces acting in three dimensions, or evaluating the motion of objects in a 3D environment. A thorough understanding of this concept enables the solution of complex problems in physics, engineering, and computer graphics, where vectors are indispensable.

Applications in Physics

Vectors and their lengths are fundamental in physics, where they describe quantities such as displacement, velocity, acceleration, and force. The length of a vector represents the magnitude of these quantities, providing a measure of their size in a given direction. Understanding vector length is essential for analyzing and solving problems related to motion and forces.

In mechanics, vectors are used to represent forces acting on an object. The length of the force vector indicates the force's magnitude, while its direction shows the force's line of action. This information is crucial for determining the net force acting on an object and predicting its motion. Similarly, velocity and acceleration vectors describe the motion of objects, with their lengths indicating speed and rate of change of speed, respectively.

The concept of vector length is also pivotal in electromagnetism, where electric and magnetic fields are represented by vectors. The length of these vectors indicates the field's strength, influencing the behavior of charged particles within the field. By understanding vector length, physicists can analyze complex phenomena, such as the motion of electrons in a magnetic field or the propagation of electromagnetic waves.

Applications in Computer Graphics

In computer graphics, vectors are essential for representing positions, directions, and transformations of objects in a virtual space. The length of a vector determines the scale of transformations, influencing the size and orientation of objects. Understanding vector length is crucial for creating realistic animations and visual effects in computer-generated imagery (CGI).

Vectors are used to represent the position of objects within a scene, with their lengths determining the distance from a reference point. They also dictate the direction of movement, with the length indicating the speed of motion. In animation, vectors are employed to calculate the trajectory of moving objects, ensuring smooth transitions between frames.

Additionally, vectors are used to simulate lighting and shading in computer graphics. The length of a vector representing a light source determines its intensity, affecting the brightness and contrast of the scene. By understanding vector length, computer graphics artists can create visually appealing and realistic images, enhancing the viewer's experience.

Applications in Engineering

In engineering, vectors are used to represent physical quantities such as force, velocity, and displacement. The length of a vector provides a measure of these quantities, influencing the design and analysis of engineering systems. Understanding vector length is crucial for solving problems related to structural analysis, fluid dynamics, and electrical circuits.

In structural engineering, vectors are used to represent forces acting on structures, such as beams and columns. The length of the force vector indicates the force's magnitude, affecting the structure's stability and load-bearing capacity. By analyzing vector lengths, engineers can design structures that withstand external loads and maintain structural integrity.

In fluid dynamics, vectors represent the velocity and direction of fluid flow. The length of the velocity vector indicates the flow speed, influencing the design of pumps, turbines, and piping systems. By understanding vector length, engineers can optimize fluid flow patterns, enhancing system efficiency and performance.

Vector Length in Calculus

In calculus, vectors and their lengths are used to analyze and solve problems related to motion and change. The length of a vector is often used to calculate the magnitude of derivatives, providing insights into the rate of change of vector quantities. Understanding vector length is crucial for solving problems involving vector fields and multivariable calculus.

In vector calculus, the length of a vector is used to calculate the magnitude of the gradient, which represents the rate of change of a scalar field. This information is essential for optimizing functions and finding critical points. By analyzing vector lengths, mathematicians can determine the direction of maximum change and solve optimization problems.

Vector length is also used to calculate the magnitude of the curl and divergence of vector fields. These quantities provide insights into the rotation and expansion of vector fields, influencing the analysis of fluid flow and electromagnetic fields. By understanding vector length, mathematicians can solve complex problems in calculus and enhance their understanding of vector analysis.

Common Mistakes and Misconceptions

When dealing with vectors and their lengths, several common mistakes and misconceptions can arise. One such mistake is confusing the length of a vector with its components. While components represent the vector's projections along the coordinate axes, the length is a scalar quantity representing the vector's magnitude.

Another common misconception is assuming that the length of a vector is always positive. While the length of a vector is a non-negative quantity, its components can be negative, representing direction. It is essential to distinguish between the vector's length and its components to avoid errors in calculations.

Additionally, some may overlook the importance of unit vectors, which have a length of one and indicate direction. Unit vectors are crucial for normalizing vectors, ensuring consistent calculations and comparisons. By understanding these common mistakes and misconceptions, one can improve their understanding of vector length and avoid errors in problem-solving.

Advanced Concepts Related to Vector Length

Beyond the basic calculation of vector length, several advanced concepts are related to vector length. One such concept is the dot product, which calculates the projection of one vector onto another. The dot product is used to determine the angle between vectors, with its magnitude influenced by the length of the vectors involved.

Another advanced concept is the cross product, which calculates the vector perpendicular to two given vectors. The magnitude of the cross product is related to the lengths of the vectors and the sine of the angle between them. This concept is used to determine the area of parallelograms and the orientation of vectors in three-dimensional space.

Understanding these advanced concepts related to vector length is crucial for solving complex problems in vector calculus and physics. By mastering these concepts, one can enhance their understanding of vector analysis and apply vector length in various contexts.

Frequently Asked Questions

What is the formula for calculating the length of a vector?

The length or magnitude of a vector is calculated using the Pythagorean Theorem. For a two-dimensional vector (x, y), the length is calculated as √(x² + y²). For a three-dimensional vector (x, y, z), the length is calculated as √(x² + y² + z²).

Why is the length of a vector always positive?

The length of a vector is a scalar quantity representing the vector's magnitude, which is always non-negative. While a vector's components can be negative, indicating direction, the length is a measure of distance and is inherently positive.

How does vector length relate to unit vectors?

Unit vectors have a length of one and indicate direction. They are used to normalize vectors, dividing each component by the vector's length, resulting in a unit vector with the same direction as the original vector.

Can the length of a vector be zero?

The length of a vector can be zero if all its components are zero. This vector is known as the zero vector and has no direction or magnitude, representing the absence of a vector quantity.

How is vector length used in physics?

In physics, vector length is used to represent the magnitude of physical quantities such as displacement, velocity, acceleration, and force. It provides a measure of these quantities, influencing the analysis and prediction of motion and forces.

What are some common mistakes when calculating vector length?

Common mistakes when calculating vector length include confusing the length with the components, assuming the length is always positive, and overlooking the importance of unit vectors. Understanding these concepts can help avoid errors in calculations.

Conclusion

Understanding the length of a vector r is fundamental to mastering vector analysis and its applications. Vectors represent quantities with magnitude and direction, and their length provides a measure of their size. From basic calculations in mathematics to advanced applications in physics, engineering, and computer graphics, the concept of vector length is indispensable.

By mastering the calculation of vector length and its applications, one can solve complex problems and enhance their understanding of vector analysis. Whether analyzing forces, optimizing fluid flow, or creating realistic animations, the length of a vector r is a crucial concept that underpins various scientific and engineering fields.

As we continue to explore the world of vectors, understanding their length and applications will remain a vital aspect of mathematical and scientific inquiry. By cultivating a robust understanding of vector length, we can unlock new possibilities and solve the challenges of tomorrow.

For further exploration of vectors and their applications, consider visiting reliable educational resources such as Khan Academy's Vectors and Spaces or other reputable educational platforms.