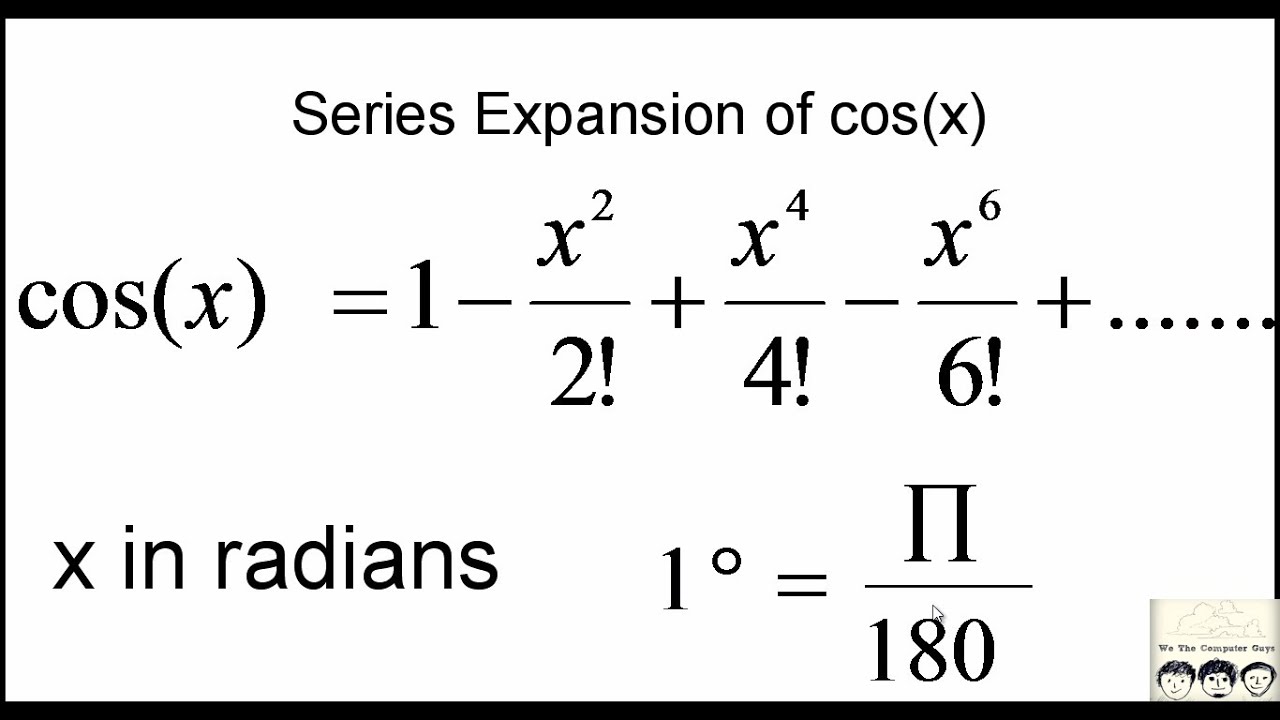The Intriguing World Of Power Series Cos: A Comprehensive Exploration

Have you ever wondered how the concept of "power series cos" fits into the grand scheme of mathematical analysis? It's fascinating to think about how these seemingly complex series can be applied to various fields such as physics, engineering, and even computer science. Understanding the intricacies of power series can open up new avenues for problem-solving and innovation. Whether you're a student, an educator, or simply a curious mind, diving into the world of power series cos can offer valuable insights and a deeper appreciation for the elegance of mathematics.

Power series, in essence, are infinite series that can represent functions in a powerful and versatile way. When we talk about power series cos, we're referring to the specific power series representation of the cosine function. This representation is not only mathematically significant but also practically useful in fields that require precise calculations and approximations. By exploring the power series cos, we unlock a tool that helps us understand and manipulate trigonometric functions in a more nuanced and comprehensive manner. The ability to represent the cosine function as a power series has profound implications across a wide range of scientific and technological disciplines.

The journey into the realm of power series cos involves understanding its derivation, properties, and applications. This exploration will take us through the historical development of power series, the mathematical principles underpinning their use, and their real-world applications. Along the way, we will also delve into related concepts such as convergence, radius of convergence, and the Taylor series, which are integral to the study of power series. Through this comprehensive guide, you'll gain a robust understanding of power series cos, equipping you with the knowledge to apply this mathematical tool effectively and confidently.

Table of Contents

• Introduction to Power Series
• Mathematical Foundations of Power Series Cos
• Derivation of the Power Series for Cos
• Properties of Power Series Cos
• Convergence and Radius of Convergence
• Applications of Power Series Cos
• Historical Perspective and Development
• Comparison with Other Trigonometric Series
• Numerical Methods and Approximations
• Power Series and Complex Analysis
• Common Misconceptions and Challenges
• Future Directions and Research
• Educational Approaches to Teaching Power Series
• Advanced Topics in Power Series Cos
• Frequently Asked Questions
• Conclusion

Introduction to Power Series

At its core, a power series is an infinite series of the form \( \sum_{n=0}^{\infty} a_n (x-c)^n \), where \( a_n \) represents the coefficients, \( x \) is the variable, and \( c \) is the center of the series. Power series are foundational in mathematical analysis and have been utilized to represent functions in a way that's both flexible and highly precise. The beauty of power series lies in their ability to approximate complex functions through an infinite sum of terms, each contributing to the overall accuracy of the representation.

Power series are not just theoretical constructs; they have practical applications in various fields. From physics to engineering, power series enable professionals to model systems and solve differential equations with impressive accuracy. They are particularly useful in scenarios where traditional algebraic methods fall short, providing a robust tool for tackling complex problems. The ability to represent functions like the exponential function, sine, and cosine as power series has paved the way for advancements in both theoretical and applied mathematics.

In the context of trigonometric functions, power series provide a unique means of representation that captures their periodic nature and infinite continuity. The power series representation of the cosine function, known as the power series cos, is a prime example of this. By expressing cosine as a power series, we gain the ability to analyze and manipulate it with a level of precision that is unparalleled by other methods. This representation is not only mathematically elegant but also incredibly practical, making it an essential tool in any mathematician's toolkit.

Mathematical Foundations of Power Series Cos

The power series representation of the cosine function is derived from the broader concept of Taylor series, a specific type of power series used to approximate functions. The Taylor series of a function \( f(x) \) about a point \( c \) is given by:

\[ f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(c)}{n!} (x-c)^n \]

For the cosine function, the Taylor series centered at zero (Maclaurin series) is particularly significant. This series is derived by evaluating the derivatives of the cosine function at zero and substituting them into the Taylor series formula:

\[ \cos(x) = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n)!} x^{2n} \]

This series is notable for its alternating nature, with each term switching between positive and negative, reflecting the oscillatory behavior of the cosine function. The factorial in the denominator ensures convergence, as it grows rapidly with each term, reducing their magnitude.

The power series cos not only provides an exact representation of the cosine function but also highlights its symmetries and properties. For instance, the even power terms in the series underscore the even nature of the cosine function, which is invariant under reflection about the y-axis. Understanding these mathematical foundations is crucial for leveraging the power series cos in practical applications.

Derivation of the Power Series for Cos

Deriving the power series for the cosine function begins with understanding its behavior and properties. The cosine function is even, periodic, and differentiable, making it an ideal candidate for power series representation. To derive its power series, we start by considering the Maclaurin series expansion:

\[ \cos(x) = f(0) + \frac{f'(0)}{1!} x + \frac{f''(0)}{2!} x^2 + \frac{f'''(0)}{3!} x^3 + \cdots \]

For the cosine function, the derivatives are as follows:

• \( f(x) = \cos(x) \), \( f(0) = 1 \)
• \( f'(x) = -\sin(x) \), \( f'(0) = 0 \)
• \( f''(x) = -\cos(x) \), \( f''(0) = -1 \)
• \( f'''(x) = \sin(x) \), \( f'''(0) = 0 \)
• \( f^{(4)}(x) = \cos(x) \), \( f^{(4)}(0) = 1 \)

Recognizing the pattern, the even derivatives contribute to the series, while the odd derivatives are zero. Substituting these values into the Maclaurin series formula gives:

\[ \cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n)!} x^{2n} \]

This derivation illustrates the elegance of the power series cos, capturing the function's periodicity and symmetry through its alternating terms and even powers. This representation is not only mathematically satisfying but also extremely useful in computational applications, where approximating the cosine function with a finite number of terms can yield accurate results.

Properties of Power Series Cos

The power series representation of the cosine function exhibits several important properties that make it a valuable tool in both theoretical and applied mathematics. One of the most significant properties is its convergence, which ensures that the series accurately represents the cosine function within a certain interval. The power series for cosine converges for all real numbers, meaning it can be used to approximate the cosine function across its entire domain.

Another key property is the series' symmetry. As an even function, the cosine function's power series consists solely of even powers of \( x \), reflecting its symmetry about the y-axis. This property is not only aesthetically pleasing but also simplifies calculations, as it reduces the number of terms needed to approximate the function accurately.

The alternating nature of the power series cos is another noteworthy feature. Each term in the series alternates between positive and negative, mirroring the oscillatory behavior of the cosine function. This alternation ensures that the series converges quickly, as the magnitude of each successive term decreases, allowing for accurate approximations with relatively few terms.

Finally, the power series cos is differentiable term-by-term within its interval of convergence. This property enables mathematicians and scientists to derive additional series representations for related functions, such as the sine function, by differentiating or integrating the power series for cosine.

Convergence and Radius of Convergence

The convergence of a power series is a critical factor determining its utility and accuracy in representing a function. For the power series cos, convergence is assured for all real numbers, as the series converges absolutely. This means that the series' terms are bounded and decrease in magnitude, ensuring the series' sum approaches the exact value of the cosine function as more terms are added.

The radius of convergence is a concept used to describe the interval within which a power series converges. In the case of the power series cos, the radius of convergence is infinite. This implies that the series converges for all real numbers and provides an accurate representation of the cosine function across its entire domain. This property is particularly advantageous, as it allows for seamless approximations and calculations in a variety of contexts.

Determining the convergence of a power series involves several tests, such as the ratio test and the root test. For the power series cos, the ratio test is commonly used to demonstrate convergence. By evaluating the limit of the ratio of successive terms, we can confirm that the series converges absolutely for all real x:

\[ \lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| = \lim_{n \to \infty} \left| \frac{x^{2(n+1)}}{(2(n+1))!} \cdot \frac{(2n)!}{x^{2n}} \right| = 0 \]

This result confirms the infinite radius of convergence for the power series cos, affirming its utility in representing the cosine function accurately across its entire domain.

Applications of Power Series Cos

The power series representation of the cosine function has numerous applications across various fields, demonstrating its versatility and practicality. One of the most prominent applications is in numerical approximation, where the power series cos is used to approximate the cosine function with a high degree of accuracy. By truncating the series to a finite number of terms, computations can be performed efficiently while maintaining precision, making it an invaluable tool in scientific computing.

In physics, the power series cos is often employed to solve differential equations and model oscillatory systems. The series' ability to capture the periodic nature of the cosine function makes it ideal for representing waveforms, harmonic oscillators, and other phenomena characterized by periodicity. Engineers also utilize the power series cos in the analysis and design of systems involving trigonometric functions, such as signal processing and control systems.

The power series cos is also instrumental in computer graphics and animation, where it is used to calculate rotations and transformations. By representing rotations as compositions of trigonometric functions, the power series cos facilitates smooth and accurate animations, enhancing the realism and fluidity of digital content.

Moreover, the power series cos plays a crucial role in complex analysis, where it is used to extend the cosine function to the complex plane. This extension enables mathematicians to explore the properties and applications of the cosine function in a broader context, leading to new insights and discoveries.

Historical Perspective and Development

The concept of power series dates back to the development of calculus and the work of early mathematicians such as Isaac Newton and Gottfried Wilhelm Leibniz. These pioneers laid the groundwork for the study of infinite series, which would later evolve into the formalized theory of power series. The exploration of power series was further advanced by mathematicians like Brook Taylor and Colin Maclaurin, who introduced the Taylor and Maclaurin series, respectively, as tools for approximating functions.

The power series representation of trigonometric functions, including the cosine function, emerged as a significant breakthrough in mathematical analysis. The ability to express these functions as infinite series allowed for more precise calculations and deeper insights into their properties and behavior. The power series cos, in particular, has been instrumental in advancing our understanding of trigonometry and its applications.

Throughout history, the study of power series has been driven by the pursuit of mathematical elegance and practical utility. The power series cos embodies this dual pursuit, offering a representation that is both mathematically rigorous and practically applicable. As mathematics continues to evolve, the power series cos remains a vital tool for exploration and discovery, inspiring new generations of mathematicians and scientists.

Comparison with Other Trigonometric Series

When examining the power series cos, it's important to compare it with other trigonometric series, such as the power series for sine and tangent. Each of these series shares common principles but also exhibits unique characteristics that reflect the properties of their respective functions.

The power series for sine, like the power series cos, is derived from the Taylor series expansion. However, the sine series consists of odd powers of \( x \), reflecting the odd nature of the sine function. This series is given by:

\[ \sin(x) = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!} x^{2n+1} \]

The alternating nature of the sine series mirrors that of the cosine series, ensuring convergence and accurate approximations. Despite the differences in their terms, both series share the property of infinite convergence, allowing them to represent their respective functions across the entire real number domain.

The power series for tangent, on the other hand, is more complex due to the function's asymptotic behavior. Unlike the power series cos and sine, the tangent series has a limited radius of convergence, making it suitable for approximations only within a specific interval around the origin.

By comparing these trigonometric series, we gain a deeper understanding of their similarities and differences, as well as the unique advantages each series offers for mathematical analysis and practical applications.

Numerical Methods and Approximations

Numerical methods play a crucial role in the practical application of power series, enabling efficient and accurate approximations of functions like the cosine function. The power series cos is particularly well-suited for numerical approximations, as its structure allows for straightforward computations with minimal error.

One common numerical method employed in conjunction with power series is Taylor polynomial approximation. By truncating the series to a finite number of terms, a Taylor polynomial can be constructed to approximate the cosine function over a specific interval. The accuracy of this approximation depends on the number of terms included, with more terms yielding greater precision.

Another numerical approach involves evaluating the remainder term of the series, known as the Lagrange remainder, to estimate the error associated with truncating the series. This method provides a means of quantifying the accuracy of the approximation, ensuring that calculations meet the desired level of precision.

In addition to these methods, power series cos can be integrated into numerical algorithms for solving differential equations and modeling physical systems. By leveraging the power series representation, these algorithms can achieve high levels of accuracy and efficiency, making them invaluable tools in scientific computing and engineering.

Power Series and Complex Analysis

The power series cos extends beyond real analysis into the realm of complex analysis, where it plays a pivotal role in exploring the properties and applications of the cosine function in the complex plane. Complex analysis is a branch of mathematics that studies functions defined on the complex number system, offering new insights and perspectives on familiar concepts.

In complex analysis, the power series cos is used to define the cosine function for complex arguments, leading to a deeper understanding of its behavior and properties. This extension allows mathematicians to explore the connections between trigonometric functions and exponential functions, as well as their applications in fields such as signal processing and quantum mechanics.

The power series cos also facilitates the study of analytic functions, which are functions that can be represented by convergent power series in some neighborhood of every point in their domain. Analytic functions possess remarkable properties, including differentiability and the ability to be uniquely defined by their power series representation.

By incorporating the power series cos into complex analysis, mathematicians can unlock new avenues for research and discovery, expanding the boundaries of mathematical exploration and application.

Common Misconceptions and Challenges

Despite its utility and elegance, the power series cos is subject to several misconceptions and challenges that can hinder its effective application. One common misconception is the belief that power series always converge to the function they represent. While the power series cos does converge for all real numbers, not all power series share this property, and some may only converge within a limited interval.

Another challenge arises from the computational complexity of evaluating power series, particularly when a high degree of accuracy is required. As more terms are added to the series, the calculations become increasingly intricate, necessitating the use of advanced numerical methods and algorithms to manage the computational load.

Additionally, the interpretation and application of power series can be challenging for those new to the concept. Understanding the nuances of convergence, error estimation, and approximation requires a solid foundation in mathematical principles and the ability to apply these concepts in diverse contexts.

To address these misconceptions and challenges, it's essential to cultivate a deep understanding of the mathematical foundations underpinning the power series cos and to develop the skills necessary to apply this knowledge effectively in both theoretical and practical settings.

Future Directions and Research

The study of power series cos continues to evolve, with ongoing research exploring new applications and theoretical insights. One promising area of research involves the development of more efficient numerical methods for evaluating power series, enabling faster and more accurate computations in fields such as engineering and physics.

Another avenue for exploration is the application of power series cos in emerging technologies, such as quantum computing and machine learning. By leveraging the power series representation, researchers can develop new algorithms and models that harness the precision and versatility of power series to tackle complex problems in these rapidly advancing fields.

In addition to these applications, future research may also focus on extending the power series cos to other mathematical domains, such as non-Euclidean geometry and topology. These extensions could lead to new insights and discoveries, expanding our understanding of the mathematical universe and its applications.

As research in power series cos continues to progress, it holds the potential to inspire innovation and drive advancement across a wide range of disciplines, reaffirming its status as a cornerstone of mathematical analysis.

Educational Approaches to Teaching Power Series

Teaching the concept of power series cos effectively requires a blend of theoretical instruction and practical application. By integrating these elements, educators can equip students with a comprehensive understanding of power series and their significance in mathematical analysis.

One effective approach is to begin with the historical context of power series, illustrating their development and applications over time. This provides students with a sense of the series' relevance and motivates their exploration of the topic.

Next, educators can introduce the mathematical foundations of power series, emphasizing key concepts such as convergence, radius of convergence, and the derivation of series for trigonometric functions. Through guided practice and problem-solving, students can develop the skills necessary to apply these concepts in various contexts.

To reinforce understanding, educators can incorporate real-world examples and applications of power series cos, demonstrating their utility in fields such as physics, engineering, and computer science. By connecting theory to practice, students gain a deeper appreciation for the power and versatility of power series.

Finally, educators can encourage exploration and experimentation, allowing students to investigate new applications and extensions of power series on their own. This fosters a sense of curiosity and creativity, empowering students to become active participants in their mathematical education.

Advanced Topics in Power Series Cos

For those seeking to delve deeper into the study of power series cos, several advanced topics offer opportunities for exploration and discovery. One such topic is the study of asymptotic expansions, which involves approximating functions by power series that converge only in the limit as the variable approaches a particular point.

Asymptotic expansions are particularly useful in fields such as physics and engineering, where they provide insights into the behavior of systems under extreme conditions. By understanding the principles of asymptotic expansions, mathematicians can develop more sophisticated models and approximations, enhancing their ability to tackle complex problems.

Another advanced topic is the application of power series cos in the study of special functions, such as Bessel functions and Legendre polynomials. These functions arise in various scientific and engineering contexts, and their power series representations offer valuable tools for analysis and computation.

Additionally, the study of power series cos in the context of differential equations presents a rich area for exploration. By examining how power series can be used to solve and approximate solutions to differential equations, mathematicians can gain new insights into the behavior of dynamic systems and develop innovative methods for analysis and control.

Through the exploration of these advanced topics, researchers and students can deepen their understanding of power series cos and its applications, expanding the boundaries of mathematical knowledge and discovery.

Frequently Asked Questions

1. What is the power series representation of cosine?

The power series representation of cosine is an infinite series that approximates the cosine function. It is given by: \(\cos(x) = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n)!} x^{2n}\).

2. Why is the power series cos important?

The power series cos is important because it allows for precise approximations of the cosine function, which is essential in various fields such as physics, engineering, and computer science.

3. How is the power series cos derived?

The power series cos is derived using the Taylor series expansion for the cosine function, evaluating its derivatives at zero and substituting them into the series formula.

4. What is the radius of convergence for the power series cos?

The radius of convergence for the power series cos is infinite, meaning the series converges for all real numbers.

5. Can the power series cos be used for complex numbers?

Yes, the power series cos can be extended to complex numbers, allowing for the exploration of the cosine function in the complex plane.

6. How is the power series cos used in numerical approximations?

The power series cos is used in numerical approximations by truncating the series to a finite number of terms, enabling efficient and accurate computations.

Conclusion

The exploration of power series cos reveals its significance as a mathematical tool with wide-ranging applications. From its mathematical foundations and properties to its practical applications in fields such as physics, engineering, and computer science, the power series cos offers a versatile means of representing and approximating the cosine function. Through a comprehensive understanding of its derivation, convergence, and utility, we can appreciate the elegance and power of this mathematical construct.

As we continue to uncover new applications and insights, the power series cos will remain an essential component of mathematical analysis and innovation. By fostering a deep understanding of this concept, we empower future generations of mathematicians, scientists, and engineers to harness its potential and contribute to the advancement of knowledge and technology.

For further reading and exploration, consider visiting external resources such as Wolfram MathWorld's Power Series page, which offers additional insights and explanations on power series and their applications.