The Comprehensive Guide To Understanding The Direction Vector Of A Line

In the world of mathematics and physics, the concept of a direction vector is fundamental to understanding how lines function in space. A direction vector essentially provides a way to describe the orientation of a line in n-dimensional space, which is crucial for various applications ranging from computer graphics to physics simulations. When we talk about a direction vector of a line, we are referring to a vector that gives direction but not necessarily magnitude. It’s like a compass guiding us along the correct path, without telling us how far we need to travel. The importance of this concept cannot be overstated, as it forms the building blocks for more complex ideas and calculations.

Understanding the direction vector of a line can often feel like trying to catch smoke with your bare hands. However, with the right approach and a clear explanation, this concept can be demystified. This comprehensive guide aims to make the direction vector of a line as accessible and understandable as possible. Through practical examples and a step-by-step breakdown, you will gain a deep insight into how direction vectors work and why they are so important. Whether you're a student looking to ace your next exam or a professional needing a refresher, this guide will serve as a valuable resource.

The direction vector of a line is not just a theoretical construct; it has real-world applications that are both fascinating and essential. From determining the trajectory of a spaceship to creating realistic animations in video games, direction vectors are at the heart of many technological advancements. This guide will not only equip you with the knowledge needed to understand direction vectors but also inspire you to explore the possibilities they offer in various fields. By the end of this article, you’ll have a solid grasp of this concept and be ready to apply it in practical scenarios.

Table of Contents

• Understanding Direction Vectors
• Mathematical Definition and Properties
• Direction Vectors in 2D and 3D Space
• Calculating the Direction Vector
• Applications of Direction Vectors
• Relationship with Other Mathematical Concepts
• Using Direction Vectors in Physics
• Direction Vectors in Computer Graphics
• Common Mistakes and How to Avoid Them
• Advanced Topics and Further Reading
• Frequently Asked Questions
• Conclusion

Understanding Direction Vectors

A direction vector is essentially a vector that points in the same direction as a line. It does not have a fixed magnitude, meaning it can be as long or as short as necessary, as long as it maintains the correct orientation. In mathematical terms, a vector is a quantity that has both direction and magnitude, but for direction vectors, it is the direction that is of utmost importance.

The concept of direction vectors is not limited to lines alone. They can also be applied to planes and other geometric objects, providing a way to describe their orientation in space. The idea is relatively simple: if you have a line in space, the direction vector tells you which way to go to stay on that line. This becomes particularly useful when dealing with problems that involve motion or changes in position.

Direction vectors are also integral to understanding vector spaces and transformations. They form the basis for operations such as vector addition, scalar multiplication, and dot products. By understanding direction vectors, you gain a deeper insight into the mechanics of vector spaces and how they can be manipulated to achieve desired outcomes.

Mathematical Definition and Properties

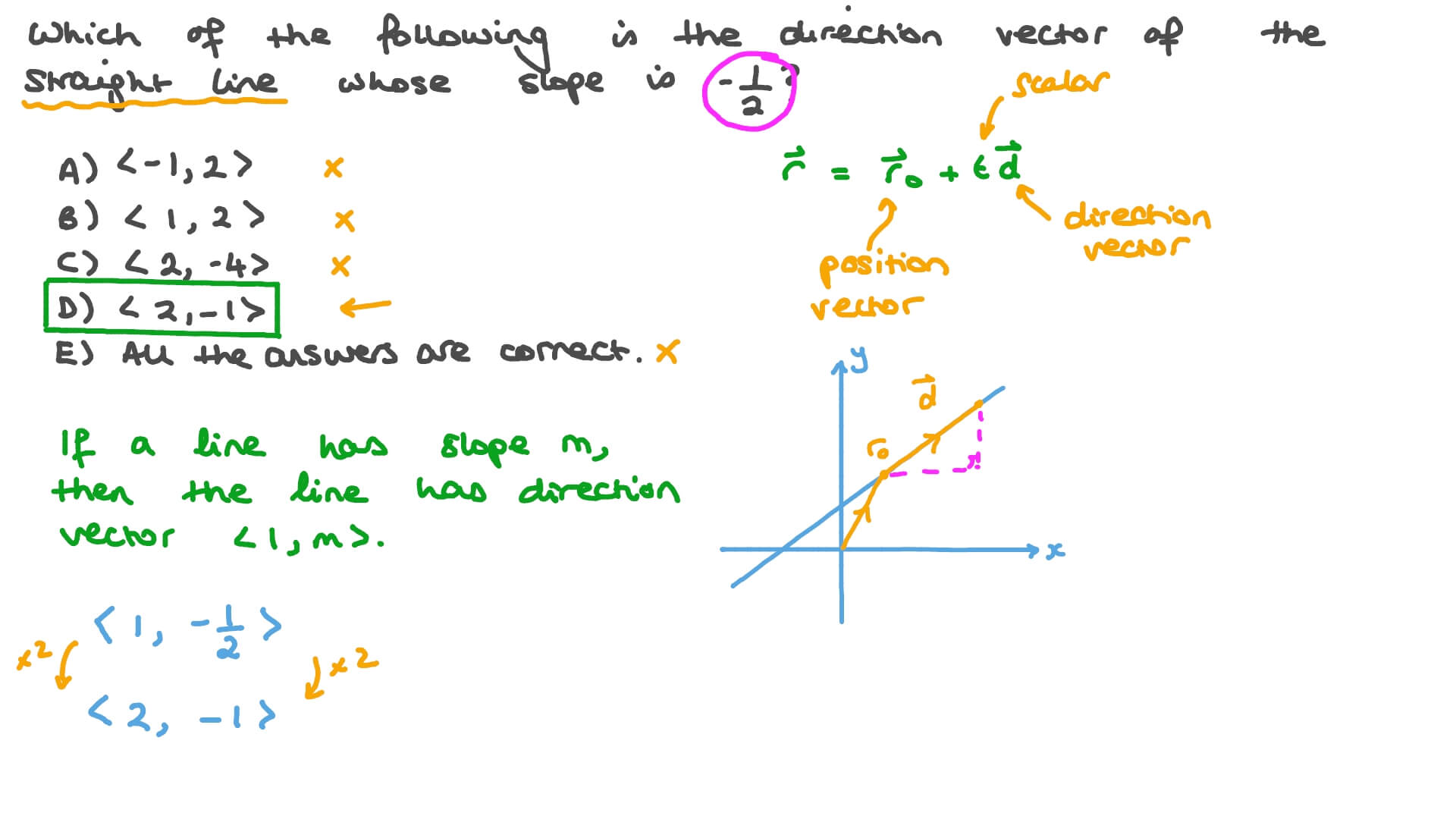
The formal mathematical definition of a direction vector is relatively straightforward. Given a line in space, the direction vector is a non-zero vector that is parallel to the line. In two-dimensional space, a line can be represented by the equation y = mx + b, where m is the slope. The direction vector for this line can be expressed as (1, m), indicating a unit step in the x-direction and m steps in the y-direction.

In three-dimensional space, a line can be represented in vector form as r = a + t*b, where a is a point on the line, b is the direction vector, and t is a scalar parameter. The direction vector b is crucial because it dictates the orientation of the line in 3D space. Importantly, the direction vector can be of any length as long as it maintains the same orientation, which means it can be normalized to have a unit length.

One of the key properties of direction vectors is their ability to be scaled. Since they only indicate direction, multiplying a direction vector by a positive scalar does not change its orientation. This property is particularly useful in applications where the magnitude of the vector needs to be adjusted without altering the direction. Additionally, direction vectors are often used in conjunction with other mathematical concepts such as cross products and dot products, allowing for more complex calculations and transformations.

Direction Vectors in 2D and 3D Space

Direction vectors can be applied in both two-dimensional and three-dimensional spaces, each with its own unique considerations. In 2D space, a direction vector can be easily visualized as an arrow pointing in the direction of a line. The components of the vector correspond to the change in x and y coordinates, providing a clear indication of the line's orientation.

In 3D space, direction vectors become more complex due to the additional dimension. Here, a direction vector is represented as a three-component vector (x, y, z), where each component represents a change in the respective coordinate. This allows for a more comprehensive description of a line's orientation in space, making direction vectors an essential tool for navigating three-dimensional environments.

The transition from 2D to 3D involves several additional considerations, such as the need to account for rotations and transformations that are unique to 3D space. Direction vectors play a crucial role in these processes, providing a means of maintaining consistent orientation even as objects are manipulated in space. By understanding how direction vectors function in both 2D and 3D environments, you can gain a more complete understanding of their applications and significance.

Calculating the Direction Vector

Calculating the direction vector of a line is a fundamental skill that is essential for solving a wide range of problems. The process involves identifying a vector that is parallel to the line, which can be accomplished through several methods depending on the context and available information.

One common approach is to use two points on the line to determine the direction vector. By subtracting the coordinates of one point from the other, you obtain a vector that points from one point to the other, effectively providing the direction of the line. This method is particularly useful when dealing with lines in a coordinate plane, as it provides a straightforward way to obtain the direction vector.

Another method involves using the line's parametric equation. In the parametric form of a line, the direction vector is explicitly given as part of the equation, making it easy to identify and utilize. This approach is often preferred in more complex scenarios where the line's equation is readily available.

Regardless of the method used, the key is to ensure that the resulting vector accurately represents the line's direction. This often involves normalizing the vector to ensure it has a unit length, which simplifies further calculations and ensures consistency across different applications.

Applications of Direction Vectors

Direction vectors have a wide range of applications across various fields, making them an invaluable tool for many professionals. In physics, direction vectors are used to describe the motion of objects, providing a means of calculating trajectories and predicting future positions. This is particularly important in fields such as aerospace engineering, where precise calculations are crucial for ensuring the success of missions.

In computer graphics, direction vectors are used to create realistic animations and simulations. By providing a way to describe the orientation of objects in space, direction vectors enable the creation of dynamic, lifelike scenes that respond to user inputs and environmental changes. This has revolutionized the gaming industry, allowing for the development of immersive experiences that captivate audiences.

Outside of these fields, direction vectors are also used in navigation, robotics, and many other areas where orientation and direction play a crucial role. Their versatility and ease of use make them an essential tool for anyone working with spatial data, offering a reliable way to represent and manipulate directional information.

Relationship with Other Mathematical Concepts

Direction vectors are closely related to several other mathematical concepts, forming an integral part of the broader study of vector mathematics. One such concept is vector addition, which allows for the combination of multiple direction vectors to produce a resultant vector that takes into account the combined effect of all the original vectors.

Scalar multiplication is another important concept that is often used in conjunction with direction vectors. By multiplying a direction vector by a scalar, you can adjust its magnitude without changing its orientation, making it possible to scale vectors to desired lengths while maintaining their direction.

Dot products and cross products are also closely related to direction vectors, providing additional tools for calculating angles and determining orthogonal vectors, respectively. These operations are frequently used in physics and engineering, where they provide a means of solving complex problems involving forces, moments, and other vector quantities.

By understanding the relationship between direction vectors and these other mathematical concepts, you can develop a deeper understanding of vector mathematics as a whole. This knowledge will enable you to tackle a wide range of problems and applications with confidence and precision.

Using Direction Vectors in Physics

In the realm of physics, direction vectors play a pivotal role in describing the motion and behavior of objects. They provide a means of representing forces, velocities, and accelerations, allowing for precise calculations and predictions. This is particularly important in fields such as classical mechanics, where direction vectors are used to model the motion of particles and rigid bodies.

In addition to their use in mechanics, direction vectors are also fundamental to the study of electromagnetism and fluid dynamics. In these areas, direction vectors are used to describe the orientation and flow of fields and fluids, providing a way to visualize and understand complex interactions.

The use of direction vectors in physics extends beyond theoretical calculations, as they are also employed in the design and analysis of experiments. By providing a clear and concise way to represent directional information, direction vectors enable scientists and engineers to design experiments that accurately capture the behavior of physical systems.

Direction Vectors in Computer Graphics

In the field of computer graphics, direction vectors are indispensable for creating realistic and dynamic visual experiences. They are used to describe the orientation of objects, cameras, and lights, enabling the creation of lifelike scenes and animations. This is particularly important in video games and virtual reality, where direction vectors are used to create immersive environments that respond to user inputs and environmental changes.

One of the key applications of direction vectors in computer graphics is the calculation of lighting and shading effects. By using direction vectors to represent the orientation of light sources and surfaces, developers can create realistic lighting effects that enhance the visual appeal of their creations.

Direction vectors are also used in camera control, providing a way to simulate realistic camera movements and transitions. This is crucial for creating engaging narratives and experiences that captivate audiences, making direction vectors an essential tool for any computer graphics professional.

Common Mistakes and How to Avoid Them

Despite their simplicity, direction vectors can sometimes lead to common mistakes that can have significant consequences. One such mistake is failing to normalize direction vectors, which can lead to inconsistent results and errors in calculations. Normalizing direction vectors ensures that they have a unit length, providing a consistent basis for further calculations.

Another common mistake is confusing direction vectors with position vectors. While both types of vectors have similar properties, they serve different purposes and should not be used interchangeably. Direction vectors represent orientation, while position vectors represent location, and confusing the two can lead to incorrect results and interpretations.

To avoid these and other mistakes, it's important to have a clear understanding of the properties and uses of direction vectors. By taking the time to thoroughly study and practice working with direction vectors, you can develop the skills and knowledge needed to use them effectively and accurately.

Advanced Topics and Further Reading

For those interested in exploring direction vectors further, there are many advanced topics and resources available. These include topics such as vector calculus, which extends the concepts of direction vectors to more complex mathematical operations and applications. Another area of interest is differential geometry, which explores the use of vectors in curved spaces and surfaces.

There are also numerous books and online resources available that provide in-depth explanations and examples of direction vectors and their applications. These resources are invaluable for anyone looking to deepen their understanding of direction vectors and their role in mathematics and physics.

By exploring these advanced topics and resources, you can expand your knowledge and skills, opening up new possibilities and applications for direction vectors in your work and studies.

Frequently Asked Questions

1. What is the direction vector of a line?

   The direction vector of a line is a vector that indicates the orientation of the line in space. It is a non-zero vector that is parallel to the line and can be scaled to any length without changing its direction.

2. How is the direction vector used in physics?

   In physics, direction vectors are used to describe the motion and forces acting on objects. They provide a way to represent velocities, accelerations, and forces, allowing for precise calculations and predictions in various physical systems.

3. Can direction vectors be used in both 2D and 3D spaces?

   Yes, direction vectors can be used in both 2D and 3D spaces. In 2D space, they are represented by two-component vectors, while in 3D space, they are represented by three-component vectors, allowing for a comprehensive description of orientation in space.

4. What is the role of direction vectors in computer graphics?

   In computer graphics, direction vectors are used to describe the orientation of objects, cameras, and lights. They enable the creation of realistic and dynamic visual experiences, enhancing the overall quality and immersion of digital content.

5. How can I avoid common mistakes when working with direction vectors?

   To avoid common mistakes, it's important to normalize direction vectors, ensuring they have a unit length. Additionally, understanding the difference between direction vectors and position vectors can help prevent confusion and errors in calculations.

6. Where can I find more information on direction vectors?

   There are numerous books and online resources available that provide in-depth explanations and examples of direction vectors and their applications. These resources are invaluable for anyone looking to deepen their understanding of direction vectors and their role in mathematics and physics.

Conclusion

The direction vector of a line is a fundamental concept that plays a crucial role in mathematics, physics, and computer graphics. By providing a way to describe the orientation of lines and other geometric objects in space, direction vectors enable a wide range of calculations and applications. Whether you're navigating the complexities of vector spaces or creating immersive digital experiences, direction vectors are an essential tool that can help you achieve your goals.

By understanding the properties and uses of direction vectors, you can develop the skills and knowledge needed to apply them effectively in your work and studies. With the right approach and resources, you can unlock the full potential of direction vectors, opening up new possibilities and opportunities in your chosen field.

Ultimately, the direction vector of a line is more than just a mathematical concept; it is a gateway to a deeper understanding of the world around us. By exploring its applications and implications, you can gain valuable insights and inspiration that will guide you on your journey of discovery and innovation.